60. n 个骰子的点数

题目链接

Lintcode

题目描述

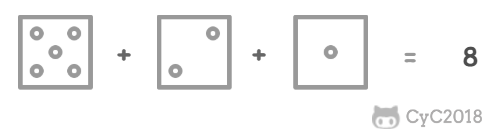
把 n 个骰子扔在地上，求点数和为 s 的概率。

解题思路

动态规划

使用一个二维数组 dp 存储点数出现的次数，其中 dp[i][j] 表示前 i 个骰子产生点数 j 的次数。

空间复杂度：O(N²)

public List<Map.Entry<Integer, Double>> dicesSum(int n) {
    final int face = 6;
    final int pointNum = face * n;
    long[][] dp = new long[n + 1][pointNum + 1];

    for (int i = 1; i <= face; i++)
        dp[1][i] = 1;

    for (int i = 2; i <= n; i++)
        for (int j = i; j <= pointNum; j++)     /* 使用 i 个骰子最小点数为 i */
            for (int k = 1; k <= face && k <= j; k++)
                dp[i][j] += dp[i - 1][j - k];

    final double totalNum = Math.pow(6, n);
    List<Map.Entry<Integer, Double>> ret = new ArrayList<>();
    for (int i = n; i <= pointNum; i++)
        ret.add(new AbstractMap.SimpleEntry<>(i, dp[n][i] / totalNum));

    return ret;
}

动态规划 + 旋转数组

空间复杂度：O(N)

public List<Map.Entry<Integer, Double>> dicesSum(int n) {
    final int face = 6;
    final int pointNum = face * n;
    long[][] dp = new long[2][pointNum + 1];

    for (int i = 1; i <= face; i++)
        dp[0][i] = 1;

    int flag = 1;                                     /* 旋转标记 */
    for (int i = 2; i <= n; i++, flag = 1 - flag) {
        for (int j = 0; j <= pointNum; j++)
            dp[flag][j] = 0;                          /* 旋转数组清零 */

        for (int j = i; j <= pointNum; j++)
            for (int k = 1; k <= face && k <= j; k++)
                dp[flag][j] += dp[1 - flag][j - k];
    }

    final double totalNum = Math.pow(6, n);
    List<Map.Entry<Integer, Double>> ret = new ArrayList<>();
    for (int i = n; i <= pointNum; i++)
        ret.add(new AbstractMap.SimpleEntry<>(i, dp[1 - flag][i] / totalNum));

    return ret;
}